Conceito de Dezena e Unidade: Uma Jornada Pelos Números

Nossa vida é cercada por números. Desde o despertar até o deitar, estamos constantemente contando, medindo e comparando quantidades. E para que essa interação seja possível, utilizamos um sistema incrivelmente versátil e poderoso: o sistema numérico decimal. Mas você já parou para pensar como aprendemos a ler e interpretar esses símbolos tão fundamentais em nosso dia a dia? Este texto visa explicar de maneira didática dois conceitos essenciais desse sistema: dezenas e unidades. Entender esses conceitos é dar os primeiros passos para navegar com confiança pelo universo dos números.

Introdução ao Sistema Numérico Decimal

O sistema numérico decimal é a base da contagem em muitas culturas ao redor do mundo, e sua importância é inquestionável. Este sistema é chamado de decimal porque é baseado em dez diferentes dígitos: de 0 a 9. Quando todos esses dígitos são utilizados, recomeçamos a contar, mas desta vez, aumentando uma casa à esquerda.

Origens e Funcionamento Básico

O sucesso deste sistema vem de uma ideia brilhante: a posição dos dígitos. Um número como 45, por exemplo, não é apenas um quatro seguido de um cinco. O 4 está na casa das dezenas, enquanto o 5 está na casa das unidades. Essa posição define seu valor real.

O Valor Posicional

O que isso significa? Em essência, cada posição, ou ‘casa’, onde colocamos um dígito dentro de um número, tem um valor dez vezes maior que a casa à sua direita. Então, no número 45:

O 5 vale realmente 5 unidades.

O 4 vale 4 dezenas, ou seja, 4 vezes 10, que equivale a 40 unidades.

Somando essas partes, chegamos ao número completo. Essa mecânica é o que chamamos de valor posicional, e é ela que permite que dez símbolos simples representem qualquer quantidade imaginável.

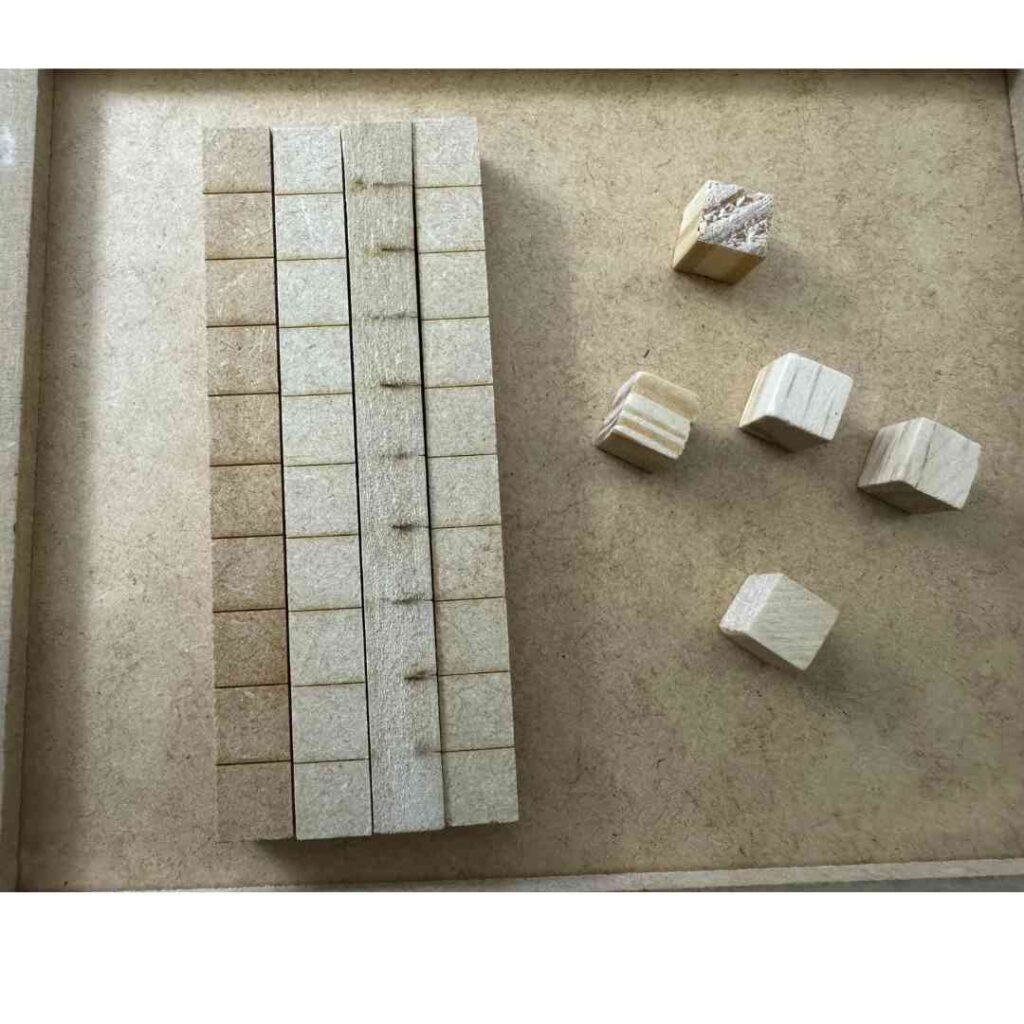
Entendendo as Dezenas: Primeiros Passos na Compreensão de Quantidades Maiores

Agora que já conhecemos a base do sistema decimal, vamos nos aprofundar no conceito de dezena.

O Significado da Dezena

A palavra “dezena” vem do latim “decem”, que significa dez. Uma dezena é literalmente um conjunto de dez unidades. Assim, quando dizemos “uma dezena”, estamos nos referindo a uma coleção de dez coisas, seja objetos, pessoas ou até mesmo dias.

Contando Dezenas

Quando contamos algo, agrupamos as unidades em conjuntos de dez para facilitar o entendimento e a visualização. Isso não é só prático; é também uma forma mais eficiente de manipular números grandes. Por exemplo, é muito mais simples dizer “três dezenas” do que “trinta”, embora signifiquem a mesma coisa.

Vejamos isso com uma analogia simples: imagine uma caixa de ovos.

Se você tem 10 ovos, tem uma dezena de ovos.
Se você tem 20 ovos, tem duas dezenas de ovos.
Se você tem 30 ovos, tem três dezenas de ovos, e assim por diante.

Cada caixa completa representa uma dezena e nos ajuda a visualizar naturalmente quantas unidades temos no total.

A compreensão desses dois conceitos – unidades e dezenas – é apenas o começo do fascinante mundo dos números. Ao compreender como esses blocos são construídos e combinados, passamos a entender melhor como funciona todo o sistema numérico decimal. Esta sólida compreensão inicial abre caminho para explorarmos a relação entre dezenas e unidades mais profundamente, bem como para começarmos a construir e decompor números com habilidade – tópicos que serão explorados adiante neste texto educativo.

O Papel das Unidades: A Base do Sistema de Numeração e a Contagem Elementar

As unidades atuam como os tijolos fundamentais da nossa estrutura numérica. Para entender o sistema numérico decimal, é essencial compreender o conceito de unidades. Simplificadamente, as unidades são a menor forma de medida numérica que não é decomposta em partes menores dentro deste sistema.

A Importância das Unidades

Imagine um conjunto de objetos — por exemplo, canetas. Se contarmos uma caneta, estamos falando de uma unidade. As unidades são indivisíveis e representam um único item ou quantidade em um dado conjunto.

1 caneta = 1 unidade
2 canetas = 2 unidades
3 canetas = 3 unidades
E assim por diante…

As unidades continuam sequencialmente até o número 9. Quando chegamos a 10, alcançamos o primeiro agrupamento maior chamado “dezena”, que será melhor explorado adiante.

Contagem Elementar

A contagem elementar é a habilidade básica em matemática que envolve incrementar ou decrementar as unidades uma a uma. É aqui que desenvolvemos a capacidade de contar objetos individual e sequencialmente.

Aprender a contar as unidades é um dos primeiros passos na educação matemática. Através da contagem, estabelecemos o relacionamento entre os números e os objetos que estão sendo contados.

Relação Entre Dezenas e Unidades: Construindo e Decompondo Números

Agora que já entendemos as unidades, podemos avançar para compreender como essas unidades se relacionam com as dezenas para formar os números como conhecemos.

Construindo Números

Uma dezena é composta por dez unidades. Assim que passamos da nona unidade, entramos no domínio das dezenas.

Exemplo de construção de números:

9 + 1 = 10 (nove unidades mais uma unidade formam uma dezena)

10 é representado como 1 dezena e 0 unidades.

Utilizando algarismos, o número 10 é escrito com um ‘1’ na casa das dezenas e um ‘0’ na casa das unidades. Isso indica que temos uma dezena e nenhuma unidade adicional.

Decompondo Números

A decomposição é o processo reverso da construção. Aqui, pegamos um número qualquer e o dividimos em dezenas e unidades, o que facilita o entendimento e a realização de operações matemáticas.

Exemplo de decomposição de número:

Decompomos o número 34 em 3 dezenas e 4 unidades.
Esse processo é visualizado como:
30 (dezenas) + 4 (unidades) = 34

Tabela de Decomposição

Para visualizar melhor o processo, vamos usar uma tabela simples:

Número	Dezenas	Unidades
11	1	1
24	2	4
37	3	7
50	5	0

Cada número na coluna da esquerda é decomposto em dezenas e unidades nas outras duas colunas à direita.

Aplicação no Dia a Dia

Entender essa relação entre dezenas e unidades é crucial para tarefas cotidianas, como contar dinheiro ou medir quantidades. Por exemplo:

Ao contar dinheiro, 2 notas de R$10 correspondem a 20 reais, que podemos decompor em 2 dezenas de reais.
Medir comprimento em centímetros envolve entender que 100 centímetros são iguais a 1 metro, que é o mesmo que dizer que temos 10 dezenas de centímetros.

A habilidade de construir e decompor números em dezenas e unidades torna-se uma ferramenta poderosa para resolver problemas matemáticos mais complexos e auxilia na compreensão profunda do valor posicional dos números dentro do nosso sistema numérico decimal.